Coulomb’s torsion balance

I once demonstrated diamagnetism for the children’s TV series Gastronuts, bringing a magnet close to one of two grapes at the ends of a straw suspended by a slender thread; like magic, the grape moved gently away. After broadcast the channel received a furious letter from a medical doctor outraged by the ‘pseudoscientific magnetic nonsense’. Drafting a reply, I started thinking about the exquisite delicacy of the torsion balance, invented by one of those late 18th century pro-am scientists who did so much to change our understanding of the world.

Charles Augustin Coulomb was a military engineer, born into a well-to-do family near Angoulême, France. In 1764 he was sent to the island of Martinique, one of the last French colonial possessions in the Caribbean, whose fortress needed strengthening. For the next eight years Coulomb would direct the works on Fort Bourbon, suffering from periodic episodes of malaria. The works were an opportunity to experiment, and Coulomb explored issues related to the strength of building materials and the friction of materials on slopes.

In 1772, he was ordered back to France where he began to submit articles to the Academy of Sciences even as he worked on the defences of Cherbourg, Besançon and the Ile d’Aix. His integration of calculus into his architectural calculations impressed its members; he began to spend more of his time linking his day job to science. This led to his book Théorie des Machines Simples, published in 1781, that won him a prize from the Academy.

But Coulomb was interested in much more than engineering. With the longitude problem very much in the air he felt that science must support global exploration. In 1777 he published a pamphlet on ‘ways to magnetise needles’. The first sentence of his Definitions and Principles reads like a manifesto for his great work: ‘If one suspends a magnetised needle by its centre of gravity such that it can spin any which way, it will soon align in a direction such that if it is disturbed it will be brought back to that same direction.’ 

The result was a delicate magnetic compass

Warming to his topic, he carefully analysed the oscillation times of magnetised steel strips when disturbed from equilibrium, and developed a mathematical model of the motion. He could now measure the magnetic moments of the strips. This led him directly to a comparison of the magnetic and the torsional forces on the horsehairs or silk threads he used to suspend his steels, using the moment of inertia of a suspended copper disc to derive the stiffness of the hair or thread. The result was a delicate magnetic compass, based on a long steel needle hanging from torsion thread, housed in a wooden box to protect it from air currents. He proposed it as an instrument to observe the diurnal variations in the Earth’s magnetic declination (the difference between geographical and magnetic north). The pamphlet earned him another prize and promotion within the academy.

In 1784 he produced another blockbuster article on the theory of steel torsion wires in which he demonstrated that the torsional force was proportional to the fourth power of the diameter and inversely proportional to the length of the wire; above all the force was proportional to the angle of torsion. He could now determine the elastic moduli of different metals. Strikingly, he began to use the term ‘balance de torsion’ part way through the paper, as he began to use his oscillatory method to measure friction in air and liquids.

A few months later Coulomb presented his new torsion balance. At its base was a glass cylinder 12 inches across with a flat glass cover pierced by two circular holes. Over the central hole was cemented a second narrower cylinder, the housing for the torsion wire, attached to an adjustable suspension mount at the top. From the wire hung a rod with a small wax-coated ball at one end and a paper counterweight-cum-damper on the other.

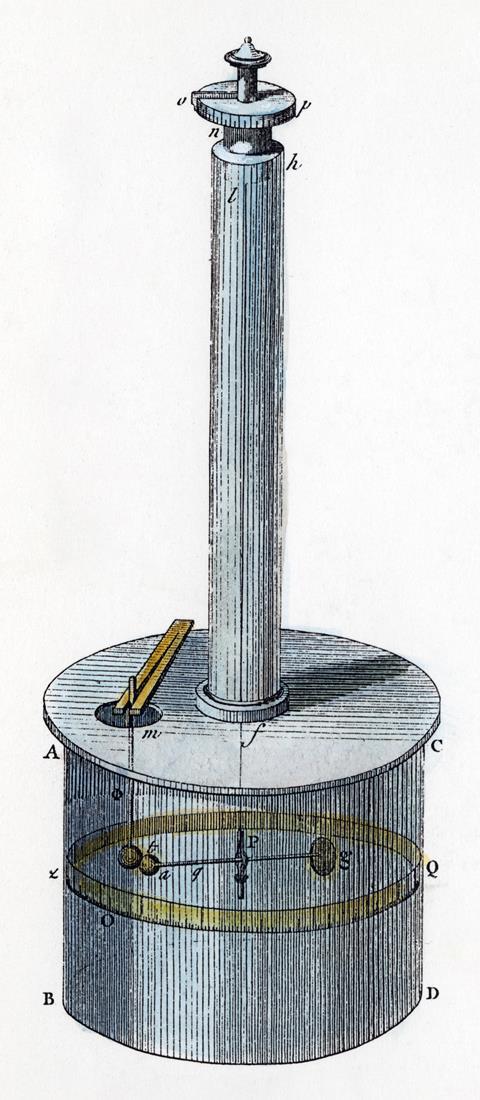
Through the second hole he could introduce an identical, but electrically charged, waxed ball, stuck on the end of a needle. Once the two balls touched they had identical charges and repelled each other, causing the suspended ball to twist away, like my grape. Coulomb could measure the precise force of repulsion from the angle of torsion. He now stated his ‘fundamental law of electricity’: that the force depends on the inverse square of the separation between the charges.

When the revolution came Coulomb fled to the quieter countryside city of Blois, leaving all his science behind until things calmed down a few years later. Almost exactly in parallel, Henry Cavendish used a torsion balance, invented independently by John Mitchell, to determine the density of the Earth. Torsion balances were here to stay.

In my reply to the doctor, I briefly mentioned the history and the revolutionary delicacy of the method, and gave detailed instructions. To my delight, a few weeks later he sent me a letter describing how he’d set up the demonstration with his daughter, and how much learning and fun they’d had. I don’t suppose Coulomb ever imagined that he would inspire children too.

Dedicated to the memory of Paul McMillan. A colleague. A teacher. A Francophile. A friend.