Turing patterns

 

During his tragically short life that began 100 years ago, Alan Turing wrote only one paper about chemistry. Published two years before his untimely death, it is arguably one of the most influential ever to have come from an outsider to the field.

As he was essentially a pure mathematician, it’s surprising that Turing had anything to say about chemistry at all. But one never knew what to expect from him. Turing’s curiosity wandered far, and he was apt to find connections between what seemed the most disparate of problems and ideas.

Turing showed how chemical reactions can create patterns. If you mix the ingredients he specified, they can separate into quasi-ordered patches of different composition. Turing’s theory of chemical pattern formation, now vindicated experimentally, looks like the best candidate for explaining a variety of puzzles in biological development, from the spontaneous differentiation of some tissues to the formation of pigmented markings and the patterns of leaves on plant stems. And his spontaneous patterning scheme is relevant beyond chemistry and biochemistry: it has been invoked to explain how sand ripples form, how ants dispose of dead bodies, how termites build their nests, and why crime is focused in ‘hotspots’.

Breaking symmetry

Born in London in 1912, Alan Turing is popularly known for his cryptographic activities at Bletchley Park during the second world war, in particular for his role in cracking the Enigma code used by the German navy. This sensitive wartime work left the authorities particularly alarmed when Turing was prosecuted in 1952 for homosexual activity, still a crime at that time. The fear was that he would be vulnerable to blackmail, and he was commanded to undertake a course of ‘corrective’ hormone therapy. Although Turing is said to have borne this cruel sentence with ‘amused fortitude’, the shame and the physical effects seem to have driven him to take his own life in 1954 by biting into an apple laced with cyanide – although there is some evidence that his death might have been accidental.

Turing’s mathematical prowess was combined with an inventiveness of mind that made him a pioneer of artificial intelligence and the theory of computation. It was essentially a mathematical question that led Turing to think about chemical patterns. He wondered how a ball of identical cells in the early stages of an embryo’s growth can develop into an organism with different features, so that some cells become limbs, some eyes, and so forth. The appearance of an organism’s body plan is called morphogenesis, and it seemed to be an example of spontaneous symmetry-breaking: from uniform to differentiated.

Turing proposed that an embryo becomes patterned into regions with different anatomical fates by chemical substances called morphogens (literally ‘shape-formers’), which diffuse through cells and tissues. He was deliberately vague about what morphogens are – they could be hormones, perhaps, or genes, the chemical nature of which was still at that point poorly understood. The key point is that they diffuse and react with one another: his scheme is what is now known as a reaction–diffusion system. Turing showed how, under certain theoretical conditions, interacting morphogens could give rise to dappled patterns made up of blobs of different chemical composition.

He realised that his scheme had broad ramifications for biology. It might, for example, account for animal markings and for the arrangement of leaves and florets in plants, called phyllotaxis. However, it now transpires that this mechanism isn’t necessary for symmetry-breaking of a fertilised egg. Instead, the symmetry is disrupted from the outset by maternal proteins diffusing from one side of the embryo. Yet, as chemist Patrick De Kepper of the University of Bordeaux in France points out, the real triumph of Turing’s paper was to show that ‘no vitalist principle is required for biological development – ordinary physical and chemical laws could do the job’.

 

 

It wasn’t obvious from the dense mathematical discussion in Turing’s paper what the key ingredients of his process were. That became apparent in 1972 when developmental biologists Hans Meinhardt and Alfred Gierer at the Max Planck Institute for Virus Research in Tübingen, Germany, devised a theory of biological pattern formation without knowing about Turing’s work. They showed that stationary chemical patterns can result from two interacting ingredients – equivalent to Turing’s morphogens – if they have specific characteristics. One is an ‘activator’, which is autocatalytic and so introduces positive feedback. The other is an ‘inhibitor’, which suppresses the autocatalysis of the activator. Crucially, they must have different rates of diffusion, the inhibitor being faster. In effect, this means that the activator’s self-amplification is corralled into local patches, while the inhibitor prevents another such patch from growing too close by. When a referee of their paper pointed Meinhardt and Gierer to Turing’s work, they found that his equations can describe just this situation.

‘The basic principle we discovered helped tremendously to understand Turing’s paper,’ says Meinhardt. ‘It also made it more straightforward to understand more complex patterning systems in biology.’ Philip Maini, a specialist on pattern formation in biology at the University of Oxford, UK, agrees: ‘I don’t believe much had happened between the 1952 paper and 1972, when Meinhardt really got stuck into the problem.’

Computer calculations of the activator–inhibitor scheme revealed that there are two generic types: spots and stripes. In both cases, the pattern features all have roughly the same size and spacing. In theory, a Turing pattern can be a perfectly ordered lattice of spots or array of stripes, but in practice, random defects interrupt this perfection, producing a quasi-regular pattern. Straight away it’s obvious why Turing’s theory looked like a good candidate for explaining the zebra’s stripes and the leopard’s spots.

Making waves

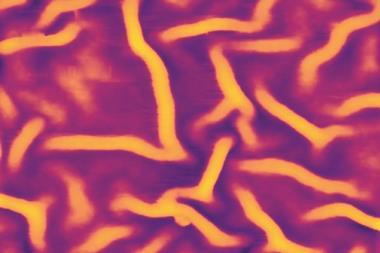
In one of those coincidences that crop up so often in science, experimental evidence for spatial patterning from a combination of chemical reaction and diffusion was being discovered at the very time that Turing was laying down the theory. In the Soviet Union during the 1950s, the chemist Boris Belousov stumbled by chance across a cocktail of reagents that oscillated back and forth between two states. As they seemed to violate the second law of thermodynamics, Belousov’s results were dismissed, and he was barely able to publish them. But in the 1960s they were explored by Anatoly Zhabotinsky, a biochemistry graduate student in Moscow interested in the rhythmic character of glucose metabolism. He found a variation of Belousov’s mixture that switched back and forth between red and blue.

 

The oscillations are another consequence of a fine balance between rates of reaction and diffusion in an autocatalytic process. The Belousov–Zhabotinsky reaction switches between two branches involving different reaction intermediates, each of which can exhaust itself by runaway feedback and thereby create the conditions for the other branch to take over. Left to its own devices, the oscillations eventually die out as the intermediates capitulate to the final products – which is why there’s no real threat to thermodynamic laws. But if the reaction is carried out in an unmixed solution, the switch doesn’t happen everywhere at once but propagates as a regular series of pulsed chemical waves, creating striking patterns.

 

‘The wave-like spread is comparable with the spread of an infection or of a forest fire,’ explains Meinhardt. Essential to the pulsed activity of the waves is the fact that once a wavefront has passed through it, a region enters a ‘refractory’ period during which it can’t support another wavelike excitation – in the forest fire analogy, this is the time taken for trees to regrow.

These chemical travelling waves are different from Turing’s stationary patterns, but the general principles of reaction and diffusion are the same. What differs are the relative rates by which the ingredients diffuse. The connections between the two systems first began to emerge in the late 1960s from the work of Russian-born chemist Ilya Prigogine and his coworkers at the Free University of Brussels in Belgium. Reaction–diffusion patterns, which Prigogine referred to as ‘dissipative structures’ because they are sustained by dissipation of energy in a non-equilibrium process, formed a central component of the work on non-equilibrium thermodynamics that earned Prigogine a Nobel prize in chemistry in 1977.

Slow motion

In the early 1970s, De Kepper began to work on these systems. He and his colleagues found a way to sustain an oscillating chemical reaction a controlled distance away from thermodynamic equilibrium, using a so-called continuous stirred tank reactor to allow a constant throughflow of reactants.

 

 

 

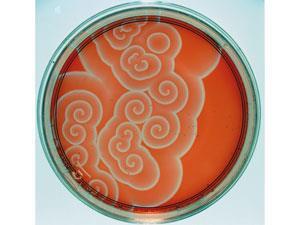
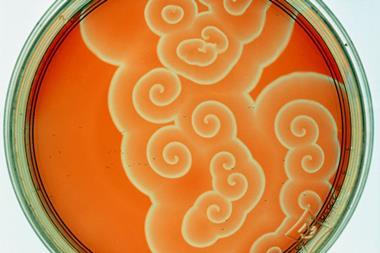
‘In the 1970s, many groups working on oscillatory chemical reactions were dreaming of producing Turing patterns,’ De Kepper explains. But although some occasionally claimed success, the patterns always turned out to be something else. Yet De Kepper stumbled upon them almost by accident. He was investigating an oscillating reaction called the chlorite–iodide–malonic acid (CIMA) reaction, which shares some ingredients with the Belousov–Zhabotinsky reaction, and in 1985 he and his colleagues had begun to look at spatial patterns in this mixture. They didn’t expect to find actual Turing structures – but in 1990, when they saw a band of spots appear in a strip of gel into which the reagents had diffused from opposite sides, they recognised them for what they were because De Kepper’s colleague Jacques Boissonade had already predicted a genuine Turing structure of this kind using computer calculations in 1988. The discovery ‘was very exciting’, says Maini. ‘By that stage, research on the subject was beginning to wane, but this gave it a great boost.’

 

The reason why these patterns appeared in the CIMA reaction was explained a year later by Irving Epstein and István Lengyel at Brandeis University in Waltham, US. The autocatalytic positive feedback in the CIMA reaction is mainly controlled by iodide ions. But the reaction uses starch as a colour indicator for iodine formed in the reaction, and iodide can become bound to iodine and starch, forming a large complex that diffuses slowly through the gel. This slowing down of the diffusion of the ‘activator’ is what brings the reaction dynamics into the regime for Turing patterns to form. De Kepper happily admits that this turned out to be a stroke of pure luck. Three years ago, he and his colleagues Judit Horváth and István Szalai described a general method for creating Turing structures in oscillatory reaction–diffusion systems by using the same trick of retarding the positive-feedback agents by complexation.

In the wild

Growing Turing’s spots and stripes in the lab is one thing – but are they really found in biology? In the 1980s, Meinhardt and mathematical biologist James Murray at the University of Washington in Seattle, US, worked independently to show that Turing’s theory offered a plausible explanation for a wide range of animal pigment patterns, from zebras to giraffes to seashells. The idea is that the morphogens turn on or off genetic pathways that stimulate the production of pigments – in mammal skins, the pigment melanin, which generates colours from tawny to black.

 

More recently, Maini and his colleagues have shown that two coupled activator–inhibitor processes can produce the broken ring markings characteristic of jaguars, while Maini’s collaborator Sy-Sang Liaw at the National Chung-Hsing University in Taiwan has demonstrated that a Turing scheme implemented on the curved shells of ladybirds can produce patterns looking very much like those seen in nature.

 

The clinching proof that animal pigment patterns are indeed Turing patterns would be to identify the morphogens involved. Although no one has succeeded in doing that, there are other types of biological pattern for which we do seem to be closing in on the likely biochemical agents underlying the process. In 2006, Thomas Schlake and his coworkers at the University of Freiburg in Germany found evidence that hair follicles in mice are arranged by a process of activation and inhibition. They proposed that a protein called Wnt is the activator of follicle formation, while proteins belonging to a class known generically as Dkk act as inhibitors of Wnt. Schlake and colleagues showed that genetic mutant mice that produce Dkk proteins in abnormally high amounts develop follicle patterns that match those predicted theoretically from Turing-style activator–inhibitor models of the diffusion and interaction of Wnt and Dkk.

Meanwhile, Meinhardt has collaborated with ornithologist Richard Prum at Yale University, New Haven, US, to show that the periodic barbs of bird feathers can be explained if the protein product of a gene called Sonic hedgehog (Shh) – a common patterning gene in many species – behaves as an activator while the bone morphogenic protein 2 is an inhibitor. Through the interaction of these components, the uniform epithelium of the developing feather bud becomes divided into a series of stripe-like ridges that prefigure its break-up into distinct barbs. And very recently, developmental biologist Jeremy Green of King’s College London, UK, and his collaborators have shown that the regularly spaced ridges of the mammalian palette seem to be arranged by a Turing-type reaction–diffusion mechanism involving the proteins Shh and fibroblast growth factor as the inhibitor and activator respectively. 

Sand, cemeteries and crime

The generic Turing stripes resemble ripple patterns in wind-blown sand. This may be no coincidence. Meinhardt suggests that, at root, the formation of these sand patterns is akin to an activator–inhibitor system. The mounds and ridges of sand are formed by deposition of wind-blown grains. As a ridge gets bigger, it enhances its own growth by capturing more sand from the air. But in doing so, it acts as a sink, removing sand from the wind and suppressing the formation of other ripples nearby. The balance between these two processes establishes a roughly constant mean distance between ripples.

 

The feedbacks involved in replication, competition and predation might set up Turing-type patterns in animal communities. Spanish physicist Ricard Solé at Pompeu Fabra University in Barcelona and his coworkers think that this might account for the patchiness of zooplankton in the sea and the phytoplankton on which they graze. And Guy Theraulaz of Paul Sabatier University in Toulouse and coworkers have found that certain Mediterranean ants pile the dead bodies of other ants into ‘cemeteries’ that can be considered Turing structures. The French researchers suspect that similar mechanisms might underlie many other aspects of habitat formation and grouping, such as nest construction, in higher organisms.

 

Perhaps even human communities, orchestrated by social feedbacks on behaviour and movement, organise themselves into Turing patterns. That’s the implication of a theory developed by US mathematician Martin Short at the University of California, Los Angeles, and his colleagues, to explain the well attested phenomenon of crime hotspots: districts in which the crime rate is anomalously high. Short’s model of ‘diffusing’ criminals and potential victims produces hotspots due to the competition of local activation (crime breeds more crime) and long-ranged inhibition (policing). 

It’s hard to guess where Turing’s patterns might turn up next. The idea that he hatched 60 years ago, as it were literally from a fertilised egg, has proved astonishingly fertile, as it turns out to be one of nature’s universal pattern-forming strategies.