Bonding accurately predicted in diatomics by new scheme

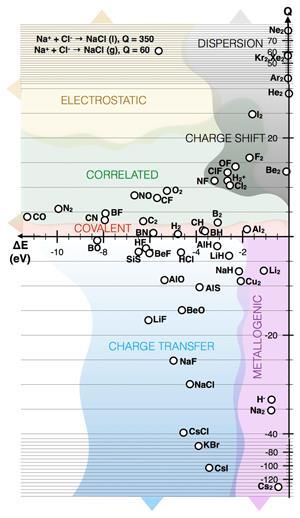
Classifying chemical bonds is one of chemistry’s necessary conceits: it introduces order among diverse molecules, but it is never an exact science. The crude division into covalent and ionic bonds can be supplemented by, for example, charge-shift bonds (a resonance between ionic forms), electrostatic interactions, dispersion forces and so on. But can all these distinctions be reliably derived from a consideration of how electrons are rearranged when atoms bind together? A new theoretical scheme proposed by Martin Rahm and Roald Hoffmann of Cornell University in Ithaca, US, shows how a single measure, plotted as a function of bond dissociation energy, can separate out all the major bond classes in diatomic molecules.¹

The researchers begin by considering the average electron binding energy in a molecule, ?¯ – a quantity identified in 1989 by Princeton chemist Leland Allen as a measure of electronegativity.² For a given molecule, this quantity can be either calculated from theory or measured experimentally. ‘Considering all electrons allows us to look at heavier elements, where the valence–core separation becomes increasingly fuzzy,’ Rahm and Hoffmann state in the paper.

But in an earlier paper they point out that the total energy of the molecule isn’t just equal to ?¯ times the number of electrons; there are two other contributions too.³ One is the repulsion energy between nuclei V_NN, which depends on the spatial arrangement of the atoms. The other is a term ? representing the ‘multi-electron interactions’, which encapsulates the way that all the electrons ‘feel’ each other’s presence.

Dissecting interactions

‘The multi-electron term ? encompasses all possible electron–electron interactions,’ Rahm and Hoffmann explain. ‘This term can be dissected into familiar categories, such as classical electrostatic repulsion, exchange repulsion, and so on. But we chose to keep them together.’

The energy of bond formation as two atoms come together, ?E, is then equal to the changes in these three terms. Different types of bond can be identified from the relative contributions to the bonding energy that the three terms make. Regardless of whether the total energy change is positive or negative (endothermic or exothermic), bond formation might then be, say, ‘nuclear-resisted’ (only ?V_NN positive) or ‘multi-electron-favoured’ (only ?? negative). This gives a new way to think about the various energy contributions.

Rahm and Hoffmann now boil the analysis down further by defining a quantity Q as the difference between n??¯ and (?V_NN+ ??) (where n is the number of electrons). This can actually be calculated just from n??¯ and ?E, and the two researchers show that different ranges of Q correspond to different bond types. Q=1 corresponds to a purely covalent bond, while negative Q indicates a large degree of ionicity. Bonds with Q>1, meanwhile, are those in which multi-electron effects become increasingly important: dispersion forces or molecules with strongly correlated electrons. Q<-1 corresponds to bonds that are polar or that give rise to metal-like behaviour in larger clusters such as in dilithium.

Anatomy of a bond

A better separation of the bond types occurs when Q is plotted against ?E. Then, for example, bonds that have a strongly correlated character, as in oxygen for instance, separate from charge-shift bonds, such as fluorine, both with positive Q. Similarly, charge–transfer or ionic bonds, such as in sodium chloride, are distinct from ‘metallogenic’ bonds, as in Na₂, both with negative Q.

‘Our method allows for approximate energy decomposition analyses without calculating electron wavefunctions or densities,’ say the researchers. Instead, it can rely on information available from spectroscopic measurements or from simpler calculations. ‘We hope that experimentalists equipped with photoelectron and vibrational spectroscopy and accurate heats of reaction or formation will use our methodology to extract approximate quantum mechanical information of reactions and chemical and physical transformations purely from experiment,’ they say. They point out that the method also allows the properties of condensed phases, such as in metals and ionic crystals, to be deduced solely from the corresponding diatomic molecules.

Inorganic chemist Santiago Alvarez of the University of Barcelona in Spain says that it’s not so easy to gain an intuitive picture of what Q means. He thinks the implications might become more apparent when the work is extended from diatomics to polyatomic molecules.

But physical chemist Ángel Martin Pendas of the University of Oviedo in Spain says it’s not obvious how to achieve that generalisation. He also thinks that Q is not easy to interpret, as it ‘mixes too many things in the same bucket’. Nevertheless, he says, the work is valuable because it ‘introduces an element that has been quite overlooked: the role of electron–electron interactions in bonding’.