Quantum chemistry simulations offers beguiling possibility of ‘solving chemistry’

Using machine learning three groups, including researchers at IBM and DeepMind, have simulated atoms and small molecules more accurately than existing quantum chemistry methods. In separate papers on the arXiv preprint server the teams each use neural networks to represent wave functions of electrons that surround the molecules’ atoms. This wave function is the mathematical solution of the Schrödinger equation, which describes the probabilities of where electrons can be found around molecules. It offers the tantalising hope of ‘solving chemistry’ altogether, simulating reactions with complete accuracy. Normally that goal would require impractically large amounts of computing power. The new studies now offer a compromise of relatively high accuracy at a reasonable amount of processing power.

Each group only simulates simple systems, with ethene among the most complex, and they all emphasise that the approaches are at their very earliest stages. ‘If we’re able to understand how materials work at the most fundamental, atomic level, we could better design everything from photovoltaics to drug molecules,’ says James Spencer from DeepMind in London, UK. ‘While this work doesn’t achieve that quite yet, we think it’s a step in that direction.’

Two approaches appeared on arXiv just a few days apart in September 2019, both combining deep machine learning and Quantum Monte Carlo (QMC) methods. Researchers at DeepMind, part of the Alphabet group of companies that owns Google, and Imperial College London call theirs Fermi Net. They posted an updated preprint paper describing it in early March 2020.¹ Frank Noé’s team at the Free University of Berlin, Germany, calls its approach, which directly incorporates physical knowledge about wave functions, PauliNet.²

Later the same month, a team including one researcher each from IBM and Flatiron Institute, both in New York, US, and the University of Zurich, Switzerland, published its machine learning approach.³ It adapts a method for simulating molecules in quantum computing to classical computers, and also uses QMC to optimise its results.

In chemistry, deep learning may be able to solve the Schrödinger equation for the electrons around atoms by finding their wave functions almost exactly, says Noé. ‘Solving the Schrödinger equation essentially means to find a function that specifies which positions of all the electrons in a molecule are more likely and which are less likely,’ he explains. It’s too difficult to calculate exact wave function solutions for anything but a hydrogen atom, but quantum chemistry algorithms can approximate them.

Conventional algorithms such as ‘coupled cluster’ methods start with evaluating a wave function component known as a Slater determinant, Noé explains. ‘If we want to be really accurate and reliable in solving the Schrödinger equation, then the sheer number of such components grows exponentially with the number of electrons. So it is no problem for five electrons, barely doable for 10, impossible for 20.’ The key challenge for many algorithms is the trade-off between efficiency and accuracy in the wave function approximation, or ‘ansatz’.

‘Neural networks have shown impressive power as accurate function approximators and promise as a compact wave function ansatz for spin systems,’ the DeepMind team writes in its arXiv paper. ‘Many groups have been using deep neural networks to solve problems in quantum mechanics,’ adds DeepMind’s David Pfau. Recent activity was triggered in 2017 by a method developed by Giuseppe Carleo and Matthias Troyer, then at ETH Zurich, he says.⁴ However, chemical systems are much harder to deal with because of the Pauli exclusion principle, where two electrons can’t be in the same place at the same time, Pfau says. ‘This introduces complicated constraints, which means you can’t just use an off-the-shelf neural network.’

Quantum Monte Carlo for the win

DeepMind therefore built a bespoke deep neural network to handle the complex calculations needed to satisfy the Pauli exclusion principle. They used a long-established method known as variational QMC.

‘To start with, you have an initial guess for the state of the system,’ explains Spencer. The estimate includes the wave function and energy of the chemical system. ‘You randomly sample possible configurations of electrons from this probability distribution, then compute the average energy of the system in all these different configurations. Then you take a small step from your initial guess to one that has a slightly lower energy, and repeat the whole process over again. You keep doing this until the energy can’t go any lower.’ Variational methods will always be above the energy of the chemical system that is part of the true solution to the Schrödinger equation, usually far above with simple versions, he adds. ‘But if you allow your guesses to become too complicated, it might be unwieldy or intractable to find the best one.’

Pfau adds that Fermi Net hits a sweet spot: just complicated enough that it can get very accurate energies, but not so complicated that it’s impossible to optimise. He and his colleagues use deep learning to train their neural network to convert properties of electrons, such as the distance from an atom’s nucleus, into wave functions. ‘You can make variational QMC methods much, much more accurate if you use deep neural networks as an approximation to the quantum state of the system – so much more accurate that you can actually match, and in some cases even exceed, the accuracy of more sophisticated methods,’ he says.

The DeepMind team claims the greatest accuracy of all the three teams. The computing power required to achieve this is neither excessive nor insignificant, with simulations of ethene taking two days of neural network training with eight graphics processing units (GPU). For example, Fermi Net predicts the dissociation curve of a nitrogen molecule to ‘significantly higher accuracy than the coupled cluster method’, says Pfau.

Noé’s team uses a similar combination of neural network and variational QMC. ‘We use deep neural networks in order to have a very flexible way to represent our wave functions,’ Noé explains. ‘The price is that the individual Slater determinants are more expensive to compute than in standard quantum chemistry. But the gain is that we need many fewer such elementary computations for example around five to 20 instead of thousands to millions to achieve the accuracy for the molecules shown in the preprint.’

However, PauliNet’s design encodes more physical knowledge about wave functions, which makes it faster. Noé’s group studied molecular hydrogen, lithium hydride, beryllium and boron atoms, and a linear chain of 10 hydrogen chain atoms. For these systems, PauliNet could reach 99.9% of the correct energy within tens of minutes to a few hours on a single GPU. With a similar number of Slater determinants, other QMC methods are much less accurate, the team writes. Density functional theory (DFT) is an exception from the normal rule of exponentially increasing computational cost, Noé says, and is therefore by far the most popular quantum chemistry method. ‘Deep QMC is more expensive than DFT, but can be much, much more accurate than other quantum chemistry methods with similar cost,’ he comments.

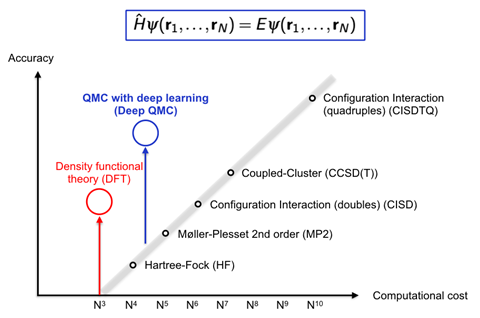
The Berlin team is now working on much bigger systems with ‘very promising results’, Noé says. ‘If we can scale quasi-accurate solutions of the electronic Schrödinger equation to 50–100 electrons we can cover a wide variety of chemistry,’ including small organic molecules, he adds. DeepMind’s Fermi Net and FU Berlin’s PauliNet ‘perform very similarly’ if you train them for the same amount of time, Noé says. PauliNet requires fewer parameters and less memory because it has a lot of physics built-in, he adds. ‘We can see a lot of possibilities to improve the method by combining ideas from both PauliNet and Fermi Net.’

Where spin comes in

Meanwhile, Carleo, having moved from ETH Zurich to the Center for Computational Quantum Physics at Flatiron Institute, has teamed up with Antonio Mezzacapo from IBM and Kenny Choo from the University of Zurich. Carleo and Troyer’s 2017 paper used machine learning to solve Schrödinger equations in lattice-based interacting quantum systems, based on spin properties, for the first time. But due to the problem with Pauli’s exclusion principle the resulting neural networks couldn’t normally be applied to electron orbitals. But Mezzacapo had been working on methods for use in quantum computing to map systems like electron orbitals onto spin-based frameworks. When Mezzacapo and Carleo met at a conference, they realised they could combine the two ideas to simulate chemistry in neural networks.

Carleo notes that unlike PauliNet and Fermi Net, his team’s approach includes a direct representation of electron orbitals.⁴ ‘For them the electron just moves in free space as a particle that can move continuously,’ he says. Otherwise the method similarly uses a neural network as the ansatz to which they apply variational QMC, Choo explains.

‘We find that this neural network can perform better than some of the more standard chemistry techniques like coupled cluster, on some molecular dimers,’ Choo says. That’s especially true in cases where the properties of electrons are highly correlated, like the dissociation of a nitrogen molecule or a pair of bonded carbon atoms, Mezzacapo adds. Carleo argues that within the chosen set of orbitals the approach is even more accurate than PauliNet and Fermi Net. ‘In the future, we will understand which one of the two philosophies is more efficient to study these molecular systems,’ he says. ‘At the moment, I would say there is not a strong argument for one or the other.’

So far the mapping approach only involves a single layer of simulated neurons, and therefore doesn’t count as deep learning, which uses a few layers. Using a more complex architecture is one of the next steps for the team, says Choo. Noé says that the mapping method complements PauliNet and FermiNet. ‘Whether the approach will scale well to large molecules is yet unclear, but it is a very elegant approach and definitely worth following up on,’ says Noé

For spin systems, Carleo has been able to take his initial 2017 results on a few particles and scale them up to simulations of thousands today. He warns that calculations of electronic behaviour are around one or two orders of magnitude harder, but is still optimistic about their prospects. ‘I think that the same thing is going to happen also in this case, hopefully, and that we will move from these first applications to larger systems,’ he says.

Pfau agrees that the approaches hold great promise. ‘It’s exciting to see so much activity in this area. Hopefully this is just the beginning.’